Hello!
I’m working on computing the reciprocal, 1/x , for values x within the range [-100, 100] using OpenFHE primitives.
I am using OpenFHE to compute 1/x, but the value of x is in the interval [-100, 100]. However, since x = 0 would cause an error, I need to divide it into two intervals:
[-100, -1] and [1, 100]. Does that mean it is impossible to compute if x falls within [-1, 1]?
Another issue is that x belongs to two intervals. How can I use EvalDivide to compute a value close to the correct 1/x?
Hi,
I think such a large interval is rather difficult for HE. When looking at 1/x in this interval we have values ranging from negative infinity to positive infinity. This can hardly be represented by a polynomial. Even with a very large degree, there still will be a large error around x=0.
So I would suggest looking if it is possible to reduce the size of your interval.
Furthermore, I recommend having a look into this publication, where the Newton-Raphson method is used. The starting values then have to be selected very carefully but it is possible to get a better approximation than with polynomials.
If I restrict the interval to [-10, 0) U (0, 10], how do I implement 1/x using OpenFHE?
Hi @yuucyf,
as previously stated, I’d consider looking into the Newton-Raphson method.
If you want to use polynomials, I do not see a simple way here. You
could think about looking into splines, but that typically requires some
kind of comparison.
Generally speaking, you could consider applying scheme switching to do a
comparison and then evaluate a polynomial for either of that two intervals.
Nevertheless, I still suggest Newton-Raphson. It can be implemented
quickly and you are then able to check if the provided accuracy suffices
for your application.
Thanks @lujoho !
I understand that in OpenFHE, the EvalDivide function can compute 1/x, but only within either positive or negative intervals such as: [-5, -1] or [1, 5].
When the sign of x (positive/negative) is unknown, it becomes impossible to set the lower bound of argument and upper bound of argument in EvalDivide.
One thing you could try (perhaps dumb, warned ^^), is to approximate
f(x) = \begin{cases}
1/x &\text{if } x > 1\\
x & \text{if } -1 \leq x \leq 1\\
-1/x & \text{otherwise}
\end{cases}
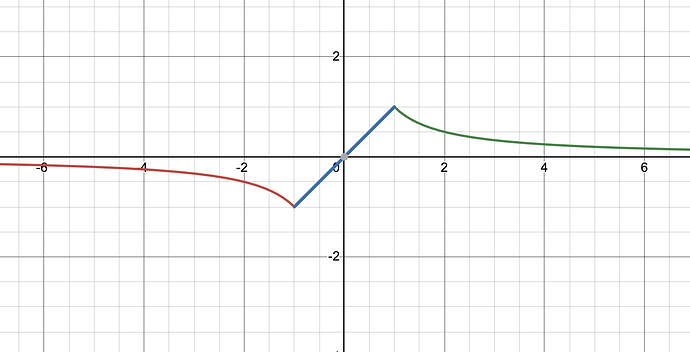
It can be horror though, I don’t think Chebyshev roots can deal with this monster without issues… but it might be worth a try – this is its plot:
It turns out that maybe is not that bad, I tried to approximate in [-4, 4] with degree 40 and looks fine
A commonly used approximate division algorithm in FHE is Goldschmidt’s division. You could give it a try.
There are a few FHE papers that used it. Check the paper Privacy-Preserving Large Language Model Inference via GPU-Accelerated Fully Homomorphic Encryption for an example.
@Caesar Thanks for sharing the link! Unfortunately, I can’t seem to access it. Is there another way you could share the information?
There was a typo in the link. Now it should work.